聯(lián)系我們(內(nèi)頁)
- 電話:15235150078
- 郵箱:1119773998@qq.com
- 網(wǎng)址:www.haiselan.com
- 地址:杏花嶺區(qū)城坊街29號院26號樓萬達(dá)兒童天地院內(nèi)(龍?zhí)豆珗@東門)
函數(shù)和導(dǎo)數(shù)是微積分中重要的概念,它們在數(shù)學(xué)和科學(xué)的各個領(lǐng)域具有廣泛的應(yīng)用。以下將討論函數(shù)與導(dǎo)數(shù)的應(yīng)用。
函數(shù)是描述兩個變量之間關(guān)系的規(guī)則。函數(shù)可以用來建立模型、預(yù)測結(jié)果和解決問題。在科學(xué)和工程領(lǐng)域中,函數(shù)經(jīng)常用于描述物理過程、經(jīng)濟(jì)關(guān)系、人口增長等。通過對函數(shù)進(jìn)行分析,可以得到函數(shù)的性質(zhì)、行為和趨勢。
導(dǎo)數(shù)是函數(shù)的變化率或斜率的度量。導(dǎo)數(shù)表示了函數(shù)在不同點上的變化方式。導(dǎo)數(shù)的計算和應(yīng)用有助于研究函數(shù)的最 值、拐點、曲線的凹凸性等特征。以下是幾個函數(shù)和導(dǎo)數(shù)的應(yīng)用示例:
-
最 優(yōu)解:導(dǎo)數(shù)可以幫助我們找到函數(shù)的極 大值和極小值。在經(jīng)濟(jì)學(xué)中,例如利潤最 大化和成本最 小化問題可以通過求解導(dǎo)數(shù)為零的情況來獲得最 優(yōu)解。
-
曲線的凹凸性:導(dǎo)數(shù)的二階導(dǎo)數(shù)可以幫助我們判斷函數(shù)曲線的凹凸性。正的二階導(dǎo)數(shù)表示曲線凹向上;負(fù)的二階導(dǎo)數(shù)表示曲線凹向下。這可應(yīng)用于最 佳擬合曲線的選擇和圖像分析。
-
高階導(dǎo)數(shù):高階導(dǎo)數(shù)提供了函數(shù)更多的信息。例如,速度是位移對時間的導(dǎo)數(shù),加速度是速度對時間的導(dǎo)數(shù)。通過高階導(dǎo)數(shù)可以深入了解和描述運動過程。
-
概率密度函數(shù):在統(tǒng)計學(xué)中,概率密度函數(shù)描述了隨機(jī)變量的概率分布。通過對概率密度函數(shù)求導(dǎo),可以計算出隨機(jī)變量的期望值和方差,并進(jìn)行概率推斷。
-
最 速下降法:在優(yōu)化問題中,最 速下降法利用導(dǎo)數(shù)的方向來尋找函數(shù)的最 小值。這在數(shù)值優(yōu)化和機(jī)器學(xué)習(xí)等領(lǐng)域有著廣泛的應(yīng)用。
函數(shù)和導(dǎo)數(shù)的應(yīng)用涵蓋了許多領(lǐng)域,包括物理學(xué)、經(jīng)濟(jì)學(xué)、工程學(xué)、統(tǒng)計學(xué)等等。它們不僅幫助我們理解和建模實際問題,還推動了科學(xué)研究和技術(shù)創(chuàng)新的發(fā)展。


 周鑫
周鑫 鄭渝涵
鄭渝涵


 微信號:
微信號: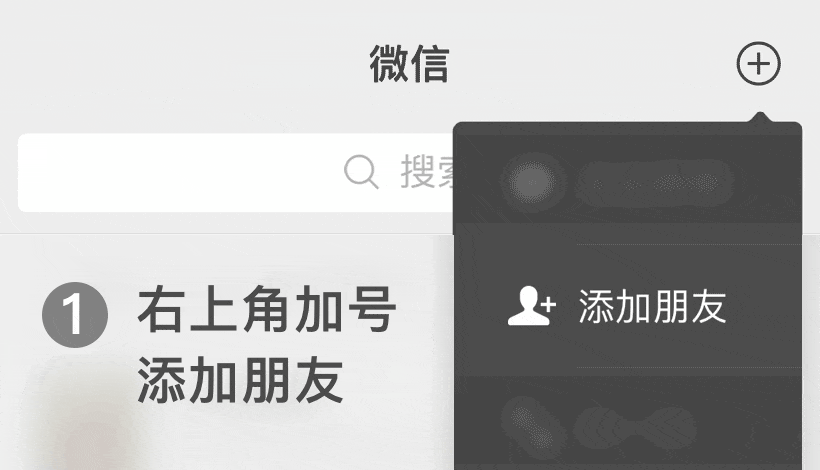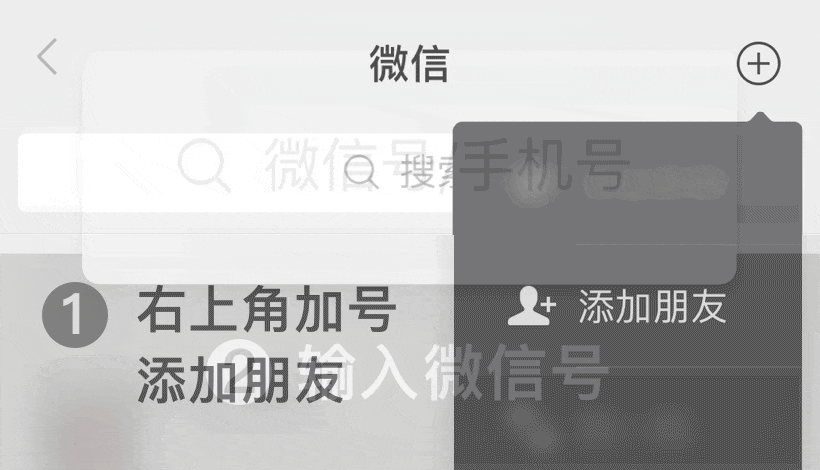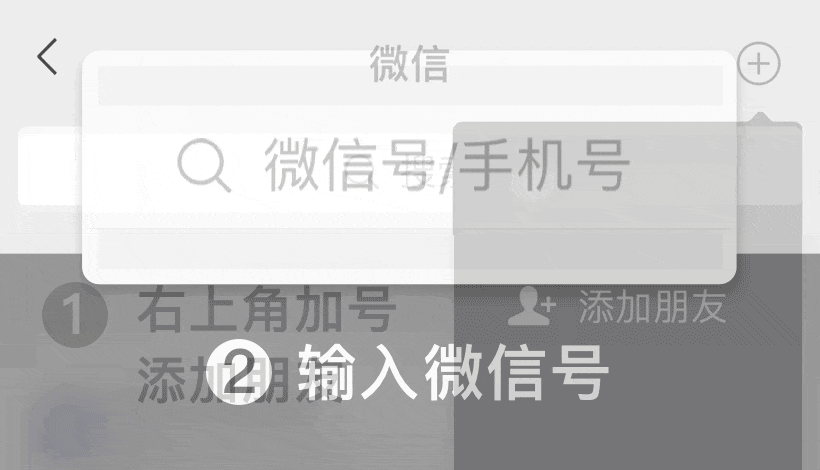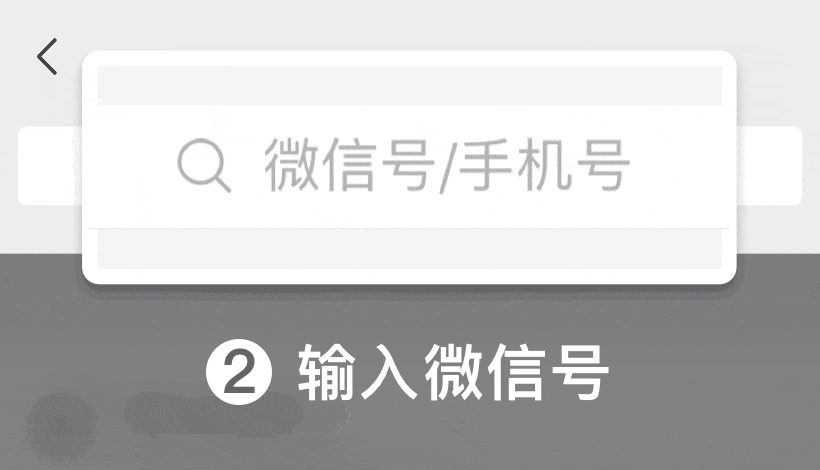
 網(wǎng)站首頁
網(wǎng)站首頁
 添加微信
添加微信
 電話咨詢
電話咨詢